Skip to content

Coordinate Transform Notes

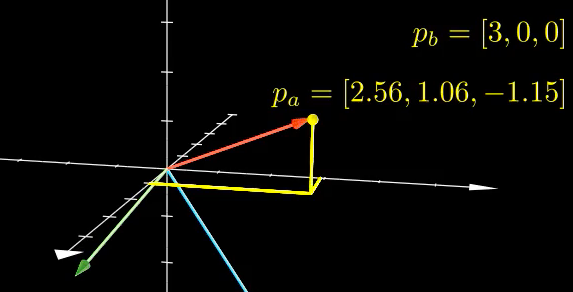
A transformation matrix is a way to map a point in one reference frame to another.

When you have pa⃗ in frame A, and want the same point, pb⃗, in frame B.pa⃗→pb⃗ Use transformation matrix MBAMBA∗pa⃗=pb⃗ Use the inverse matrix MAB to map back the other wayMAB∗pb⃗=pa⃗\text{When you have } \vec{p_a} \text{ in frame A, and want the same point, } \vec{p_b} \text{, in frame B.} \\ \vec{p_a} \rightarrow \vec{p_b} \\ \ \\ \text{Use transformation matrix } M_{BA} \\ M_{BA} * \vec{p_a} = \vec{p_b} \\ \ \\ \text{Use the inverse matrix } M_{AB} \text{ to map back the other way} \\ M_{AB} * \vec{p_b} = \vec{p_a} \\

The animation below shows an example of two frames: the white set of axis (frame A), and a multicolor set of axis (frame B) which are rotated to no longer aligns with frame A. Any point in space can be expressed relative to frame A or relative to frame B. A transformation matrix is how you get from one frame to the other.

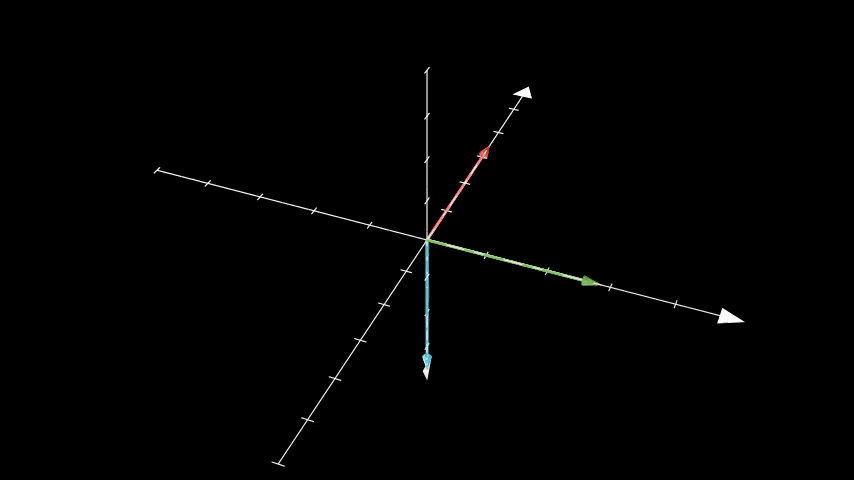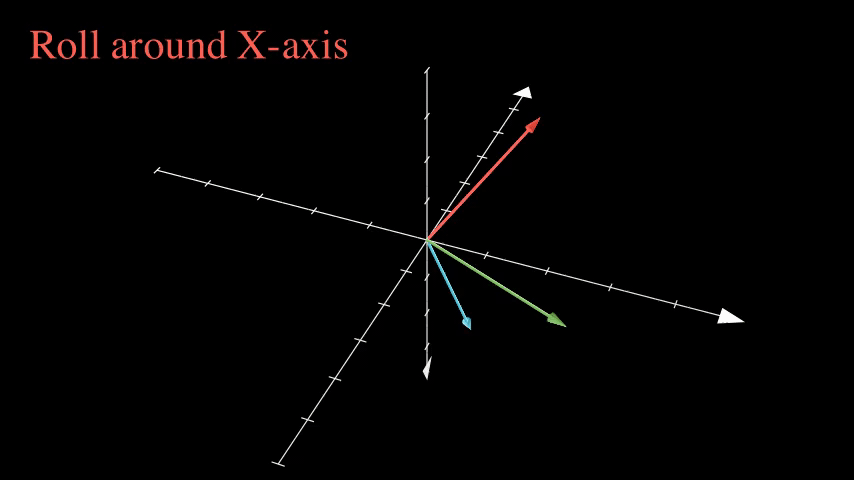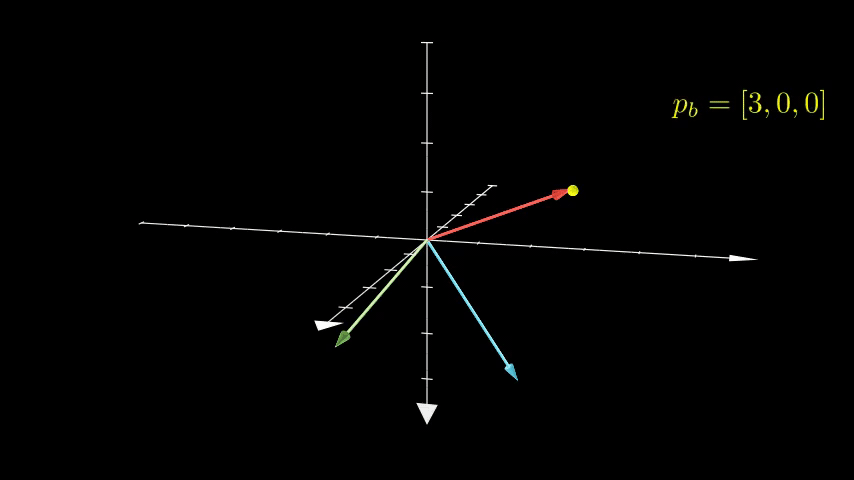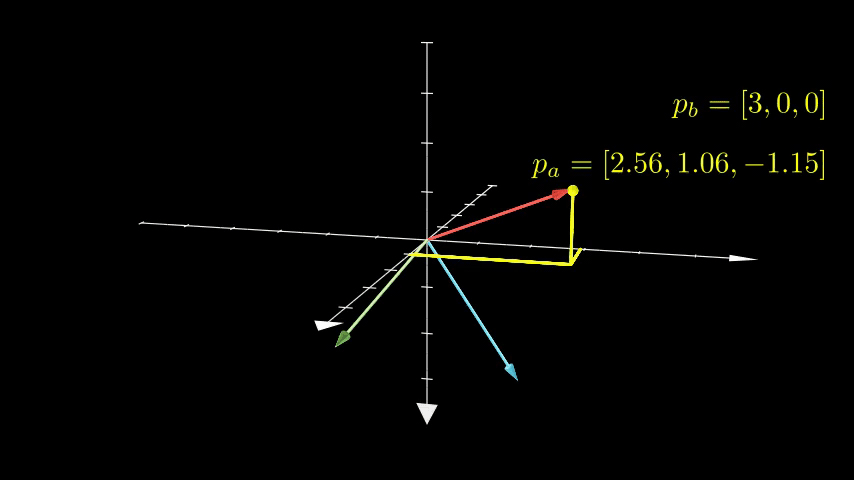
Animation created with Manim.

Coordinate Transform Matrix From Euler Angles

The matrix MAB can be calculated from Euler angles (yaw/psi, pitch/theta, & roll/phi) that define frame B relative to frame A. This matrix is generated by multiplying three component rotation matrices (Y, P, & R).

The order of multiplying the component matrices makes a difference. In this case the order of rotation going from frame A to B is yaw, pitch, roll.

Yaw: Rotate frame B about it’s own Z axisPitch: Rotate frame B about it’s own Y axisRoll: Rotate frame B about it’s own X axis Y=[cos(ψ),−sin(ψ),0sin(ψ),cos(ψ),00,0,1] P=[cos(θ),0,sin(θ)0,1,0−sin(θ),0,cos(θ)] R=[1,0,00,cos(ϕ),−sin(ϕ)0,sin(ϕ),cos(ϕ)] MAB=Y∗P∗R\text{Yaw: Rotate frame B about it's own Z axis} \\ \text{Pitch: Rotate frame B about it's own Y axis} \\ \text{Roll: Rotate frame B about it's own X axis} \\ \ \\ Y = \begin{bmatrix} cos(\psi), -sin(\psi), 0 \\ sin(\psi), cos(\psi), 0 \\ 0, 0, 1 \end{bmatrix} \\ \ \\ P = \begin{bmatrix} cos(\theta), 0 ,sin(\theta) \\ 0, 1, 0 \\ -sin(\theta), 0, cos(\theta) \end{bmatrix} \\ \ \\ R = \begin{bmatrix} 1, 0, 0\\ 0, cos(\phi), -sin(\phi) \\ 0, sin(\phi), cos(\phi) \end{bmatrix} \\ \ \\ M_{AB} = Y * P * R

MAB can transform a point in frame B (we’ll call it pb) to the same point in frame A (we’ll call it pa) by multiplying MAB on the left side of pb.

So doing this:pa⃗=MAB∗pb⃗ Is the same as doing this:pa⃗=Y∗P∗R∗pb⃗\text{So doing this:} \\ \vec{p_a} = M_{AB} * \vec{p_b} \\ \ \\ \text{Is the same as doing this:} \\ \vec{p_a} = Y * P * R * \vec{p_b}

To reverse the process and transform a point from frame A to B, use the inverse matrix, MBA, which conveniently is just the transpose of MAB.

The transpose of a transformation matrix automatically takes care of reversing the order and direction of the component rotations.

MBA=(MAB)−1=(MAB)T =(Y∗P∗R)T=RT∗PT∗YT =R−1∗P−1∗Y−1  So doing this:pb⃗=MBA∗pa⃗ Is the same as doing this:pb⃗=R−1∗P−1∗Y−1∗pa⃗M_{BA} = (M_{AB})^{-1} = (M_{AB})^T \\ \ \\ = (Y*P*R)^T = R^T*P^T*Y^T \\ \ \\ = R^{-1}*P^{-1}*Y^{-1} \\ \ \\ \ \\ \text{So doing this:} \\ \vec{p_b} = M_{BA} * \vec{p_a} \\ \ \\ \text{Is the same as doing this:} \\ \vec{p_b} = R^{-1}*P^{-1}*Y^{-1} * \vec{p_a}

A Bit About Basis Vectors

The columns of MAB (and rows of MBA) are also the basis vectors (3D axis) of frame B with respect to frame A.

Likewise the columns of MBA (and rows of MAB) are the basis vectors of frame A with respect to frame B.

xb⃗:x-axis of frame Bwith respect to frame Ayb⃗:y-axis of frame Bwith respect to frame Azb⃗:z-axis of frame Bwith respect to frame A MAB=[xb⃗T;yb⃗T;zb⃗T] MBA=[xb⃗yb⃗zb⃗]\vec{x_b} : \text{x-axis of frame B} \\ \text{with respect to frame A} \\ \vec{y_b} : \text{y-axis of frame B} \\ \text{with respect to frame A} \\ \vec{z_b} : \text{z-axis of frame B} \\ \text{with respect to frame A} \\ \\ \ \\ M_{AB} = [\vec{x_b}^T; \vec{y_b}^T; \vec{z_b}^T] \\ \ \\ M_{BA} = \begin{bmatrix} \vec{x_b} \\ \vec{y_b} \\ \vec{z_b} \end{bmatrix}

So when you transform a point in frame A to frame B you are essentially taking the dot product of that point with each basic vector of frame B.

pb⃗=MBA∗pa⃗=[xb⃗yb⃗zb⃗]∗pa⃗ =[xb⃗⋅pa⃗,yb⃗⋅pa⃗,zb⃗⋅pa⃗]\vec{p_b} = M_{BA} * \vec{p_a} = \begin{bmatrix} \vec{x_b} \\ \vec{y_b} \\ \vec{z_b} \end{bmatrix} * \vec{p_a} \\ \ \\ = [\vec{x_b} \cdot \vec{p_a}, \vec{y_b} \cdot \vec{p_a}, \vec{z_b} \cdot \vec{p_a}]

Example

Given the Euler angles of

  • yaw: pi/4
  • pitch: -pi/4
  • roll: 0

MAB can be calculated.

MAB=Y∗P∗R =[1(2),−1(2),01(2),1(2),00,0,1]∗[1(2),0,−1(2)0,1,01(2),0,1(2)] =[0.5,−1(2),−0.50.5,1(2),−0.51(2),0,1(2)] M_{AB} = Y * P * R \\ \ \\ = \begin{bmatrix} \frac{1}{\sqrt(2)}, -\frac{1}{\sqrt(2)}, 0 \\ \frac{1}{\sqrt(2)}, \frac{1}{\sqrt(2)}, 0 \\ 0, 0, 1 \end{bmatrix} * \begin{bmatrix} \frac{1}{\sqrt(2)}, 0, -\frac{1}{\sqrt(2)} \\ 0, 1, 0 \\ \frac{1}{\sqrt(2)}, 0, \frac{1}{\sqrt(2)} \\ \end{bmatrix} \\ \ \\ = \begin{bmatrix} 0.5, -\frac{1}{\sqrt(2)}, -0.5 \\ 0.5, \frac{1}{\sqrt(2)}, -0.5 \\ \frac{1}{\sqrt(2)}, 0, \frac{1}{\sqrt(2)} \end{bmatrix} \\ \ \\

Now you can use MAB to transform any point in frame B into frame A.

pb⃗=[10,2,−3] pa⃗=[0.5,−1(2),−0.50.5,1(2),−0.51(2),0,1(2)]∗[10,2,−3]T =[5.086,7.914,4.950]\vec{p_b} = [10, 2, -3] \\ \ \\ \vec{p_a} = \begin{bmatrix} 0.5, -\frac{1}{\sqrt(2)}, -0.5 \\ 0.5, \frac{1}{\sqrt(2)}, -0.5 \\ \frac{1}{\sqrt(2)}, 0, \frac{1}{\sqrt(2)} \end{bmatrix} * [10, 2, -3]^T \\ \ \\ = [5.086, 7.914, 4.950]

From MAB you can also get the basis vectors of frame B with respect to frame A.

xb⃗=[0.5,0.5,1(2)]yb⃗=[−1(2),1(2),0]zb⃗=[−0.5,−0.5,1(2)] \vec{x_b} = [0.5, 0.5, \frac{1}{\sqrt(2)}] \\ \vec{y_b }= [-\frac{1}{\sqrt(2)}, \frac{1}{\sqrt(2)}, 0] \\ \vec{z_b} = [-0.5, -0.5, \frac{1}{\sqrt(2)}] \\ \ \\

To get more intuition on how transformation matrix rows & columns are basis vectors you can transform a point along the x-axis in frame B into frame A. Note that the calculated value of pa found is the same value of the first column of MAB. This is because pb corresponds to the frame B x-axis relative to frame B, and pa corresponds to the frame B x-axis relative to frame A. They are, of course, the same point described from two different frames of reference.

pb⃗=[1,0,0]  pa⃗=Mab∗pb⃗ =[0.5,−1(2),−0.50.5,1(2),−0.51(2),0,1(2)]∗[1,0,0]T =[0.5,0.5,1(2)]\vec{p_b} = [1, 0, 0] \\ \ \\ \ \\ \vec{p_a} = M_{ab} * \vec{p_b} \\ \ \\ = \begin{bmatrix} 0.5, -\frac{1}{\sqrt(2)}, -0.5 \\ 0.5, \frac{1}{\sqrt(2)}, -0.5 \\ \frac{1}{\sqrt(2)}, 0, \frac{1}{\sqrt(2)} \end{bmatrix} * [1, 0, 0]^T \\ \ \\ = [0.5, 0.5, \frac{1}{\sqrt(2)}]

Rotation Direction Note

The rotation direction used follows the right-hand rule convention. With your right hand point your thumb in the direction of the axis of rotation and curl your fingers. The direction of rotation your fingers are curling is the positive rotation direction about that axis.

The original uploader was Schorschi2 at German Wikipedia., Public domain, via Wikimedia Commons
Tags:

Leave a Reply

Your email address will not be published. Required fields are marked *